这周读了一篇论文《基于LASSO和神经网络的量化交易智能系统构建》,借机看了一下Lasso的概念。做点笔记以备复习。
Lasso 全称Least absolute shrinkage and selection operator。主要的作用是regularization,也就是防止overfitting。通常用在linear regression和logistic regression里。说到regularization,另一种方式是ridge regression。两种表现形式如下:
- Ridge:
- Lasso:
Ridge和Lasso最重要的区别是,Ridge regression只能将不相关variables的beta减小至接近0;而Lasso regression则可以将beta减小至0。另外,需要注意的是Ridge Regression是无偏的,而Lasso则是有偏的(biased)。
那为何要用lasso呢?由于Lasso的特性—能够将无关variables的beta减少至0,因此它具有feature selection的能力。它能自动识别出哪些variables对模型的预测起到作用。
下面这副图解释了为何Lasso能将无关variables的beta减少至0。
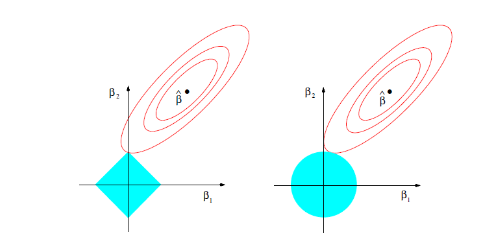
右边是Ridge regression,左边是Lasso regression。等高线的中点β hat代表了最优拟合点,但是,这个点通常是会造成overfitting的。为了避免overfitting,必须对beta的取值做出限制。也就是蓝色的区域。由图可见,Lasso区别Ridge的地方在于Lasso的beta取值范围是一个正方形,而Ridge则是圆形。在加入了regularization后的最优点一定落在红色等高线和蓝色区域相切的位置。而Lasso的切点一般会是正方形的顶点。也就是说,某些variables的beta取值为0。因此,Lasso具有feature selection的能力。
在看下图:
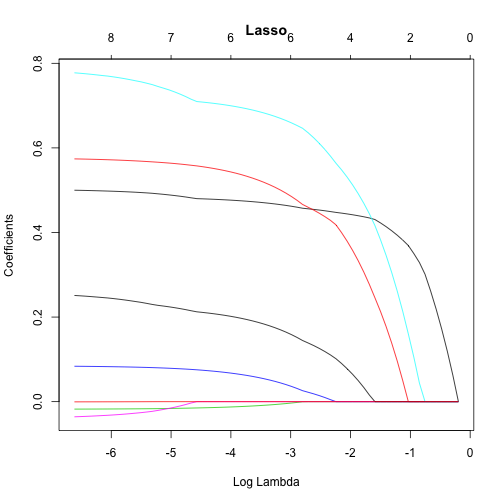
横轴代表了λ(hyper parameter)的取值范围,纵轴代表了variables的数量。从图上可以看到,在λ取值较小的时候,所有的variables都包括在了模型内,而随着λ的增加,模型里的variables不断减少。因此,当遇到variables非常多的情况(模型复杂),Lasso是可以帮助识别出哪些variables对模型影响最大。
如何确定λ的值?通常使用cross validation的方式。根据不同的λ在cross validation set上所得到的误差来确定合理的值。
最后还是要吐槽一下国内博士的水平。个人觉得这篇论文质量不怎么样,也许是期刊《投资研究》本身水平不行?该博士第一步用linear regression + lasso 来选择feature(各种股票技术指标),第二步,这些通过lasso筛选出来的featrue被用于神经网络。最后得出的结论是lasso + 神经网络在预测股市涨跌方面的效果最好,sharpe ratio最高。我能看到的一个明显的逻辑上的问题是lasso是用在linear regression上的,也就是说这一步feature selection体现的线性相关性。而神经网络可用于非线性关系的发掘。那么在第一步中筛选出来的是线性显著的技术指标,这一步很可能把非线性的关系给过滤掉了。然后在第二步中,把这些线性显著的技术指标在输入给神经网络,那是希望从已知的线性关系中进一步发掘非线性关系?!觉得逻辑上挺混乱的。