摘要:本文论述了Risk Partity的基本概念,并介绍了如何通过量化的方法构建Risk Parity的Portfolio,并以excel作为工具实现一个简单的Risk Parity的应用。
关键字:Risk Parity, Risk contribution
“不要将鸡蛋放在同一个篮子里”告诉我们要分散风险,个人觉得是一句无比智慧的话。在没有修炼成巴菲特之前我觉得还是要牢牢记住这句话。如何做到分散风险?60%的股票+40%的债券算是分散风险吗?不妨做一个情景假设,你有100w元资金,60w买入股票ETF,40w买入债券ETF,持有 1年后,假如股票下跌了10%,而债券收益2%,那么你的投资总额变成了60w0.9+40w1.02=95.88;相当于总资产减值了4.14%,这似乎是不太理想的,尤其是在股票和债券的correlation还是负相关的情况下。在以上情形下,如果加大债券的配置那么整个portfolio就会更加的平稳。那么接下来的问题就是该如何分配股票和债券的权重?
Risk Contribution
单个risk asset可以用variance来度量风险,而要计算一个投资组合的variance的话还需要知道convariance。假设这些数据是已知的。
- 组合中包括2种asset的情况:
还是假设60%股票+40%债券,并进一步假设股票的volatility是15%,债券的volatility是5%,correlation为0.2。那么根据公式: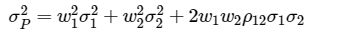
就可以计算出组合的variance: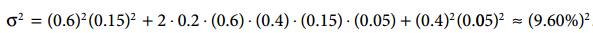
有了组合的variance,又该如何计算股票和债券对该组合variance的占比呢?观察以上的计算式,第一项可归因到股票,第三项可归因到债券。那么第二项(convariance)该如何归因呢?其实就是将一半归因到股票另一半归因到债券!
由此可知,股票的 risk contribution: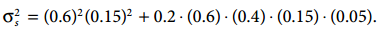
债券的risk contribution: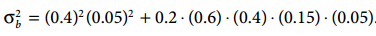
有了这些数据,接下来就能很容易计算出股票和债券在组合variance中的占比,也就是risk contribution的占比。
股票的风险占比: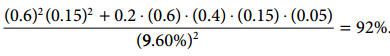
债券的风险占比: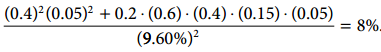
从以上数据就可以清晰的看出60/40其实是一种非常不平衡的组合,其中股票的risk contribution高达92%,也就是说在60/40的组合里面,风险主要集中在股票上。
- 组合中包括3种asset的情况:
再来讨论一下组合中持有3中资产的情况,因为3中资产的情况更具一般性,可以推广到持有更多资产的情况。假设新增资产为商品,volitility 和 correlation见下表: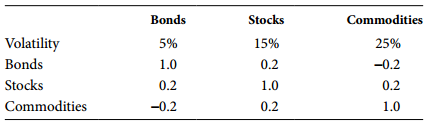
并假设按照40%的股票,40%的债券,20%的商品来分配。根据以下公式可以获得组合的variance: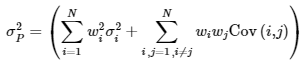
以本例的3种asset来说,可以获得如下的计算公式: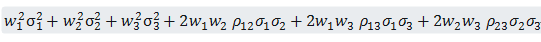
代入上表中的数据,可得出计算出组合的variance: 0.00778
接下来要求每一项资产的risk contribution, 可以通过如下方式获得: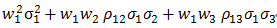
第一项是variance, 第二和第三项分别对应covariance的一半。根据以上算式可计算出:
- 债券的risk contribution:0.00044;占比:0.00044/0.00778=6%
- 股票的risk contribution:0.0044;占比:0.00444/0.00778=57%
- 商品的risk contribution:0.0029;占比:0.0029/0.00778=37%
以上数据显示,40%的债券对应的risk contribution只是6%,而股票和商品的risk contribution则显得太高了。
Risk Parity
Risk Parity (也叫risk budgeting),是通过调整各asset在组合中所占的比重以实现个asset的risk contribution相同或等于指定的数值。
- 组合中包括2种asset的情况:
这种情况很简单了,不需要考虑2种asset的correlation, 只需要比较他们的volitility就行了,再使用之前的例子,因为股票的volatility是15%,债券的volatility是5%,那么,通过让债券的volatility对应的金额增至现在的3倍即能实现股票和债券的volatility对应的金额相等。从组合比重的角度来说,也就是1%的股票要对应3%的债券,所以,组合的权重就为:75%的债券 + 25%的股票。
- 组合中包括3种asset的情况:
这种情况会比上面复杂,因为没有直接的计算方法,需要通过数值分析法来获得近似解。这里通过excel solver举例,如下图所示: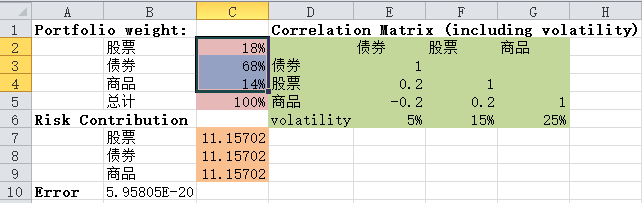
最终的解为:股票18%,债券68%,商品14%。接着对excel的输入输出做一些说明。绿色部分是correlation matrix,作为输入参数。红色部分是solver的“可变单元格”,也就是最终的输出(参见下图)。“约束条件”设置成“总计”=1 并勾选“非负数”(参见下图)。棕色部分即risk contribution是根据组合的比重计和correlation matrix算出来的,比如股票部分的计算设置成:1
=(C2^2*F6^2+C2*C3*E4*E6*F6+C2*C4*F5*F6*G6)*10000
注意这里有意将最终的计算结果放大了10000倍,这么处理是便于处理Error项,因为risk contribution的值都很小。Error项作为solver的“设置目标”,也就是优化要达到的最终目标。由于优化的目标是希望Risk contribution的各项都相同,那么也就是说这3项对应的variance=0,因此,Error就设置成:=VAR.P(C7:C9)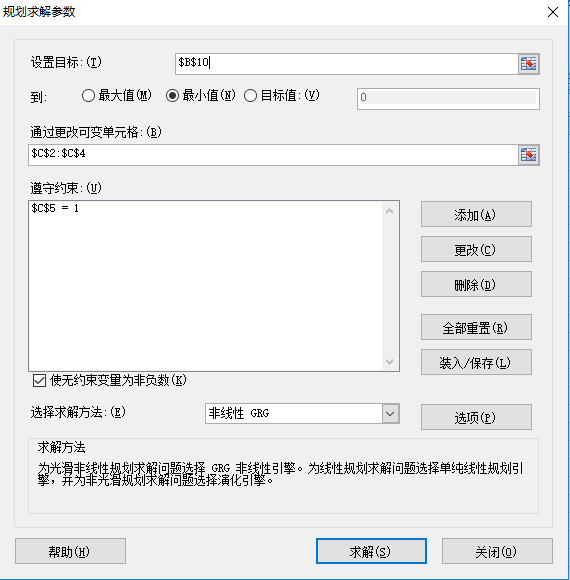
结论
本文介绍了实现risk parity的一种量化方法。并通过使用Excel的solver实现了组合中包含3类asset的risk parity的计算。以3类资产为基础很容易推广至更多类资产。个人觉得用excel+solver的方式对于组合里面asset数量在10多个的情况下是足够应付了。Risk Parity本身计算所需的输入其实很简单,就是各类asset的variance和correlation matrix。但是,所谓garbage in garbage out。如何获取可靠的variance和correlation其实倒是一个难点。
参考文献:
- 2017 CFA level1 volumn 4 corporate finance and portfolio management
- Edward E. Qian, Risk Parity Fundmentals